笔者在复习信号与系统的时候,拜读了乐正友老师的《信号与系统例题分析》,再结合自己大学四年来的课程领悟,总结出了一些比较有趣的关联性紧密的知识点。
1、带通滤波器的两种理想型
考虑如下框图和幅频响应:
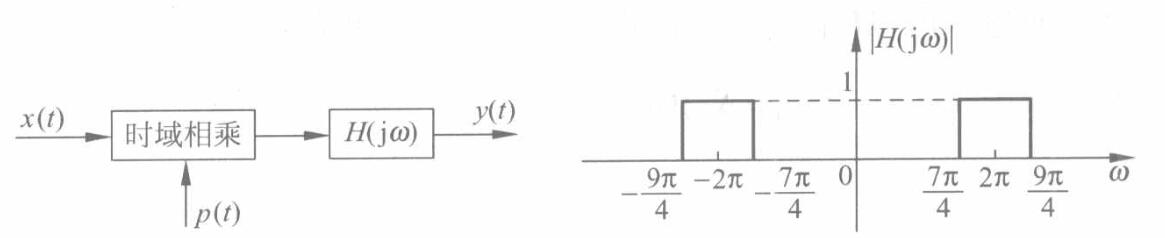
考虑如下相频响应:
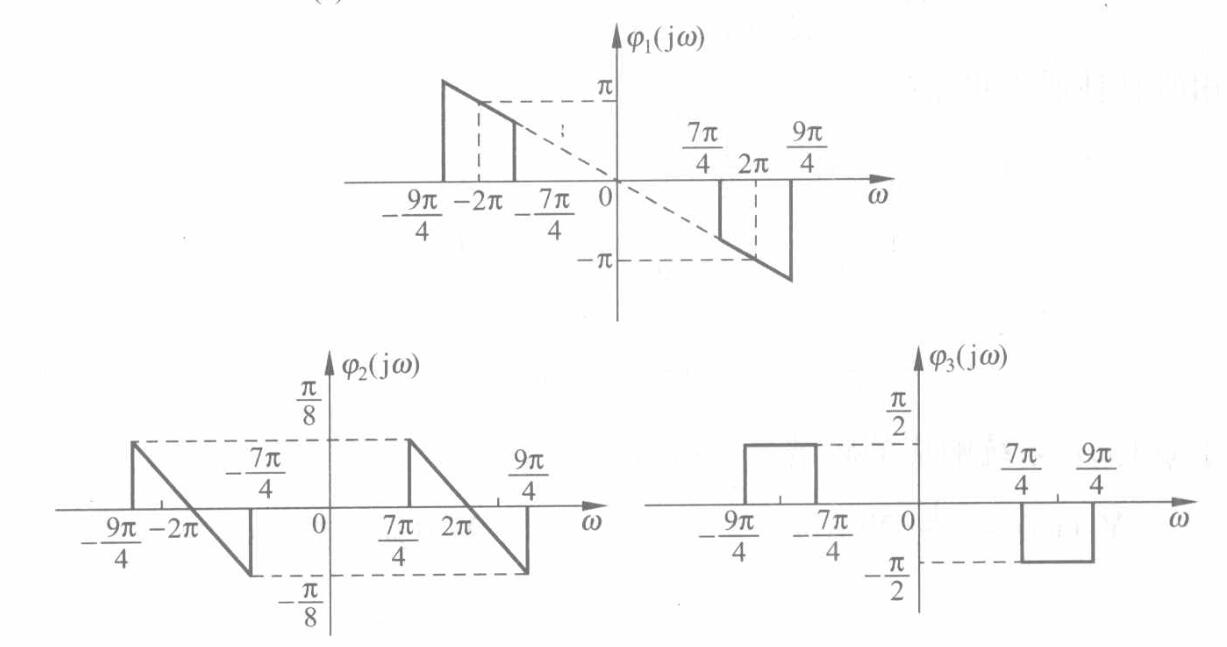
由题目条件可知:
$$
P(jw)=\frac{\pi}{2}\sum\delta(w-\frac{n\pi}{2}); \
X_s(jw)=\frac{1}{2\pi}X(jw)*P(jw)=\frac{1}{4}\sum X(w-\frac{n\pi}{2})
$$
因此,抽样信号中仅有n=4和n=-4的频谱。
(1) 相位1
相位1是严格的线性相位,因此我们可以猜想,当信号通过带通滤波器后,对于不同的频率分量,滤波器对他们的相位响应是附加上对应的相位。滤波后的信号,波形和包络都不失真。
$$
Y_1(jw)=\frac{1}{4}X(w+2\pi)e^{-jw/2}+\frac{1}{4}X(w-2\pi)e^{-jw/2}
$$
根据傅里叶变换的性质可得:
$$
y_1(t)=-\frac{1}{2}x(t-\frac{1}{2})cos(2\pi t)=\frac{1}{2}x(t-\frac{1}{2})cos[2\pi(t-\frac{1}{2})]
$$
(2) 相位2
相位2是分段线性的,因此我们可以猜想,滤波后的信号,波形失真,包络无失真。
$$
Y_1(jw)=\frac{1}{4}X(w+2\pi)e^{-j(w+2\pi)/2}+\frac{1}{4}X(w-2\pi)e^{-j(w-2\pi)/2}
$$
根据傅里叶变换的性质可得:
$$
y_1(t)=\frac{1}{2}x(t-\frac{1}{2})cos(2\pi t)
$$
(3) 相位3
该情况不再做探讨。
(4)结论
严格线性相位会对载波和调制信号同时做相移,此时波形无失真,自然包络也无失真。
分段线性相位对于载波而言没有相移,因此包络不变,但此时调制信号相移导致波形失真。
上述两种相位在采用包络检波法时都是理想的。
2、单边带调制SSB的实现
SSB单边带调制的原理框图如下。
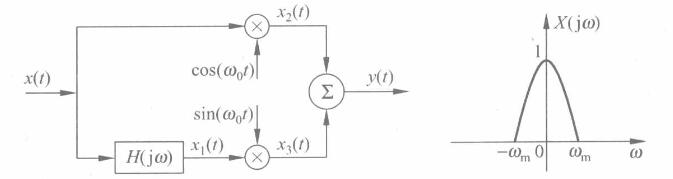
上路的余弦信号实现频谱搬移,下路一个希尔伯特变换器实现±j的相位,再乘一个正弦信号又实现j的相位。因此下路最终结果是一边频率实现同相一边频率实现反相。
中间信号频谱如下:
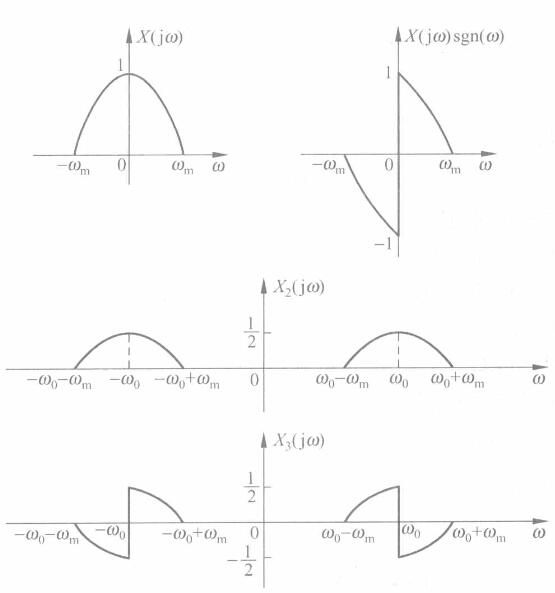
值得注意的是:
$$
X_1(jw)=-jsgn(w)X(jw)
$$
$$
X_3(jw)=\frac{j}{2}(X_1(w+w_0)+X_1(w-w_0))=\frac{1}{2}(sgn(w-w_0)X(w+w_0)+sgn(w+w_0)X(w-w_0))
$$
输出信号频谱如下:
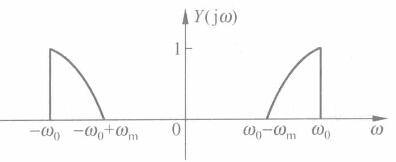
3、OFDM模型介绍
对于无线传输信道,多径效应是信道引起传输信号失真的重要原因之一。而消除多径效应的常见方法有均衡和多载波调制(MCM)技术。
均衡:实质是努力寻找与信道模型相应的逆系统,试图使信道与均衡器组合能提供逼近理想传输特性的系统模型。也可以认为是期望利用均衡器来抵消信道非理想特性引入的失真。
多载波调制(MCM)技术:MCM利用一组(N个)子载波在信道中并行传输信号,它将待传送的高速数据流分解成一组并行传输的低速数据流。每个子载波传送的数据率只是原有单载波系统的1/N,也即每个子载波承载的码元周期是原单载波系统码元周期的N倍,这就使得每个子载波传输码元的周期可以远大于信道的时延扩展,从而具有很强的抗码间干扰能力。
很早以前,人们就已经认识并利用多载波技术,但存在许多矛盾未能很好解决。传统的多载波传输构成原理与频分复用类似。高速码流经串并转换构成N个低速码流之后,分别对N个子载波进行调制。各子载波信号占据互不交叠的频率范围。这种系统需要大量的带通滤波器和调制解调器,这使系统的复杂度和成本大大提高,鲁棒性也较差。同时,为了降低邻近载波信号之间的相互干扰,各子载波之间必须留出足够裕量的保护频带,因而使系统的频谱利用率大大降低。
OFDM:要求各子载波相互正交。在接收端用正交运算(匹配滤波)技术将频谱相互重叠的子载波信号逐个分离。正交运算大致为:与发射机对应的子载波与接收信号做相乘后积分(信号内积),再进行后续信号分离。
从本质上将,OFDM技术是将在时域上相距很窄、频域占据很宽的比特流变换成频域上相距很窄、时域占据很宽的比特流。因此,对于脉冲噪声这种时宽很窄的干扰信号对OFDM比特流的影响就相对被削弱了。
下图为OFDM实现的硬件框图:
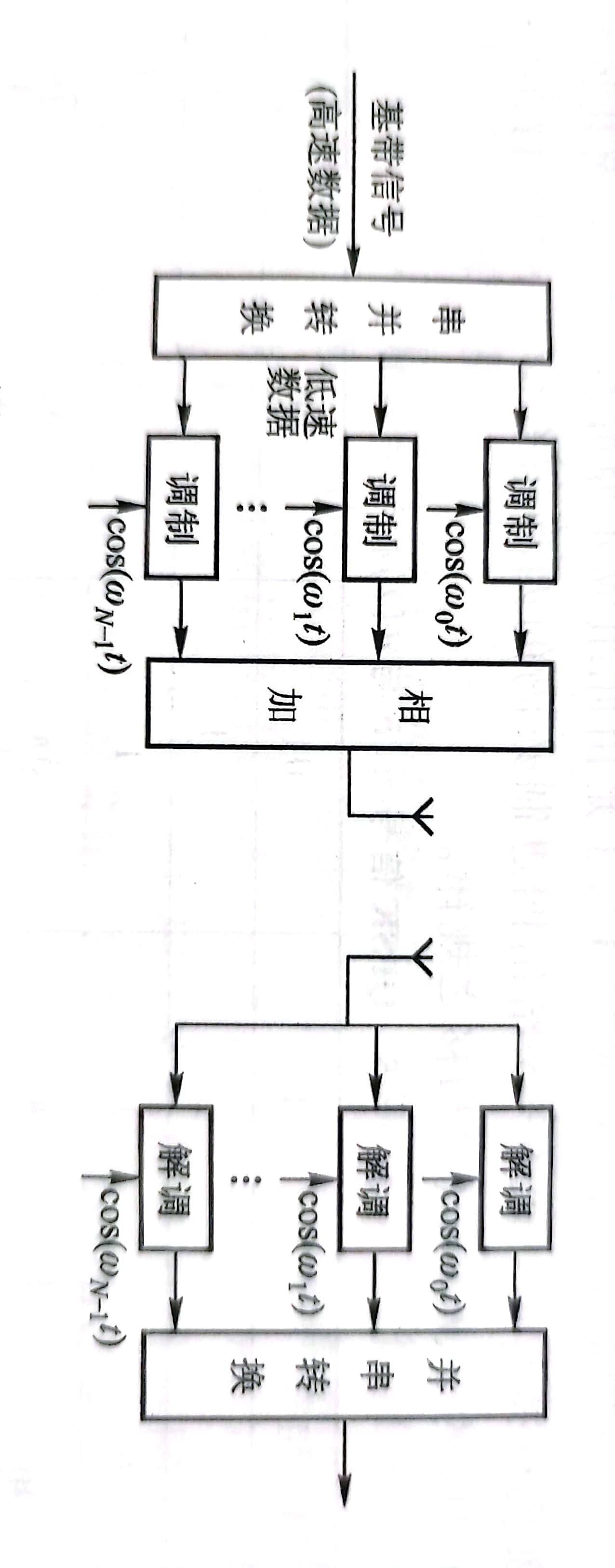
可见,硬件实现结构复杂。
4、OFDM模型的DFT(FFT)改进
考虑使用QPSK数字调制子载波的方式讨论DFT实现OFDM的原理。
每路的已调信号(该路子载波频率为w0)可写作:
$$
d(t)=acos(w_0t)+bsin(w_0t), a=\pm1,b=\pm1
$$
则N路子载波合成的OFDM信号表达式为:
$$
x(t)=\sum [a_ncos(w_nt)+b_nsin(w_nt)], a_n=\pm1,b_n=\pm1
$$
下面对x(t)进行时域抽样,间隔时间为T=Ts/N,则抽样时刻t=kT,则:
$$
x(k)=\sum [a_ncos(w_nt)+b_nsin(w_nt)]=Re(\sum (a_n-b_nj)(cos(w_nt_k)+jsin(w_nt_k))
$$
$$
=Re(sum (a_n-b_nj)e^{jw_s(\frac{kT_s}{N})})=Re(\sum (a_n-b_nj)e^{j(\frac{2\pi}{N})kn})=Re(IDFT[D(n)])
$$
其中D(n)=an-jbn,它是QPSK调制信号的复数共轭表示,完全由基带信号决定,或者说它携带了基带信息。
很明显,从以上推导可以看出,在发射端我们只要对D(n)进行IDFT运算即可产生OFDM信号。其功能完全可以取代大量振荡器与调制器构成之硬件系统。可以证明,在接收端对此信号进行DFT运算即可恢复D(n),从而获得原始之基带信息。为达此目的,需要对 DFT取2N点抽样,抽样间隔为T/2N。可见,这一方法使接收系统也大大简化。以上分析为OFDM系统的数字化提供了理论依据。传统观念中各子载波分别需要许多模拟前端的方式可以由一个共同的 DFT运算所代替,从而极大地降低了系统的复杂度。随着超大规模集成(VLSI)系统技术的发展,出现了价格低廉、结构简单的FFT专用集成电路芯片以及通用数字信号处理器(DSP)芯片,这就使OFDM系统的付诸应用成为现实。
5、数字滤波器的结构特点
直接1型:先实现系统零点再实现系统极点。
直接2型:先实现系统极点再实现系统零点。
- 优点:延时单元个数等于差分方程阶数,是延时单元最少的实现,有时候也称为典范结构实现。
- 缺点:在阶数比较高的情况下,要求系数精度高,调整特性不方便,每一系数的变化都将影响零极点的分布。
级联型:H=H1H2…Hn
- 优点:最少延时单元实现;每个二阶或者一阶子系统单独控制零极点,因而便于调整,同时在系数量化时对系统的性能影响小。子系统的前后次序对有限字长引起的量化效应时有影响的,需要仔细定夺。
- 缺点:尽管是最少延时单元实现,乘法次数明显比直接型多。
并联型:H=H1+H2+…+Hn
- 优点:对输入信号并行滤波,运行速度快;没有前后级误差累积,有限子长效应引起的量化效应小;部分分式展开后,极点可以单独调整。
- 缺点:零点无法单独调整,当需要准确控制滤波零点时就不能采用并联型结构。
6、匹配滤波器
引入:在通信系统的接收部分中,为了保证信息传输的准确性,需要设计一种“最佳检测器”,能够使有用信号增强,同时抑制噪声,保证在判别信号出现时具有最低的错误概率。
匹配滤波器:能够以最低的错误概率判决信号脉冲的有无的滤波器称为匹配滤波器。匹配指的是滤波器的特性和信号的特性取得某种一致,使得滤波器输出端得信号瞬时功率与噪声平均功率之比最大(信噪比最大)。
结论:
- 匹配滤波器的冲激响应是所需信号s(t)对垂直轴(所谓y轴)镜像并向右平移T,这样的线性系统称为匹配滤波器,匹配滤波器是线性系统的最佳滤波器。
- 匹配滤波器的功能相当于对s(t)做自相关运算,在t=T时刻取得自相关函数得峰值,峰值大小等于信号s(t)的能量E,而与波形无关。
- 所谓”最佳“仅限于线性系统。
